LRU 案例
LRU 算法描述:
LRU是Least Recently Used的缩写,即最近最少使用,是一种常用的页面置换算法,选择最近最久未使用的页面予以淘汰。该算法赋予每个页面一个访问字段,用来记录一个页面自上次被访问以来所经历的时间 t,当须淘汰一个页面时,选择现有页面中其 t 值最大的,即最近最少使用的页面予以淘汰。
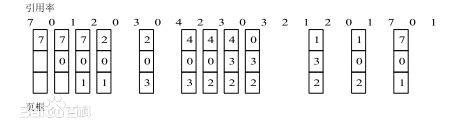
具体实现
如图所示,测试数据为{7, 0, 1, 2, 0, 3, 0, 4,2,3,0,3,2,1,2,0,1,7,0,1}
下面会给出 LRU算法的四种实现方案.
数组实现
思路: 头插尾删
维护一个数组 list, 默认容量为3, 维持一个插入元素(或访问元素)放在list[0], 删除元素(最近未使用元素)放在list[2], 即头部插入,尾部删除的思路.
时间复杂度分析:
- set() -> o(n)// 需要遍历数组判断插入位置.
- get() -> o(n)// 查找, 优化思路二分查找
- remove()-> o(n)// 移动元素.
- travel() -> o(n)// 遍历list
性能分析:
LRU 存在频繁的插入删除操作即 写多读少,导致数组移动次数过多.因而导致时间复杂度过高, 所以想到了用 链表来实现这个过程.
代码实现:
- 代码地址
package LRU;
/**
* @program: JUC
* @description: lru 数组实现,set复杂度 o(n)
* @author: WhyWhatHow
* @create: 2020-05-03 07:09
**/
public class DemoLRUArray {
/**
* lru算法实现: 最近最短时间内未被访问的数据被淘汰
*/
private Object[] list = new Object[MAX];
private Integer size = 0;
private final static Integer MAX = 3;
/**
* 查找元素, 需要重写T的equals方法
*
* @param t
* @return
*/
private int get(Object t) {
for (int i = 0; i < list.length; i++) {
if (t.equals(list[i])) {
return i;
}
}
return -1;
}
private void remove(int index) {
for(int i = index; i>0; i--){
list[i]=list[i-1];
}
}
private void set(Object t) {
int length = list.length;
// 判断插入元素是否在链表中, 是则移动元素,
int index = this.get(t);
if (index != -1) {
// 移动元素
this.remove(index);
list[0] = t;
return;
}
// 判断链表是否已满,满,删除末尾元素,队列大小不变
if (size == MAX) {
this.remove(MAX-1);
list[0] = t;
return;
} else {
// 不满则插入
this.remove(size);
size++;
list[0] = t;
return;
}
}
private void travel() {
for (Object t : list) {
System.out.print(t + ",");
}
System.out.println();
}
public static void main(String[] args) {
Integer[] a = new Integer[]{7, 0, 1, 2, 0, 3, 0, 4,2,3,0,3,2,1,2,0,1,7,0,1};
DemoLRUArray lru =new DemoLRUArray();
for (int i = 0; i < a.length; i++) {
lru.set(a[i]);
System.out.print("add "+ a[i]+": ");
lru.travel();
}
}
}
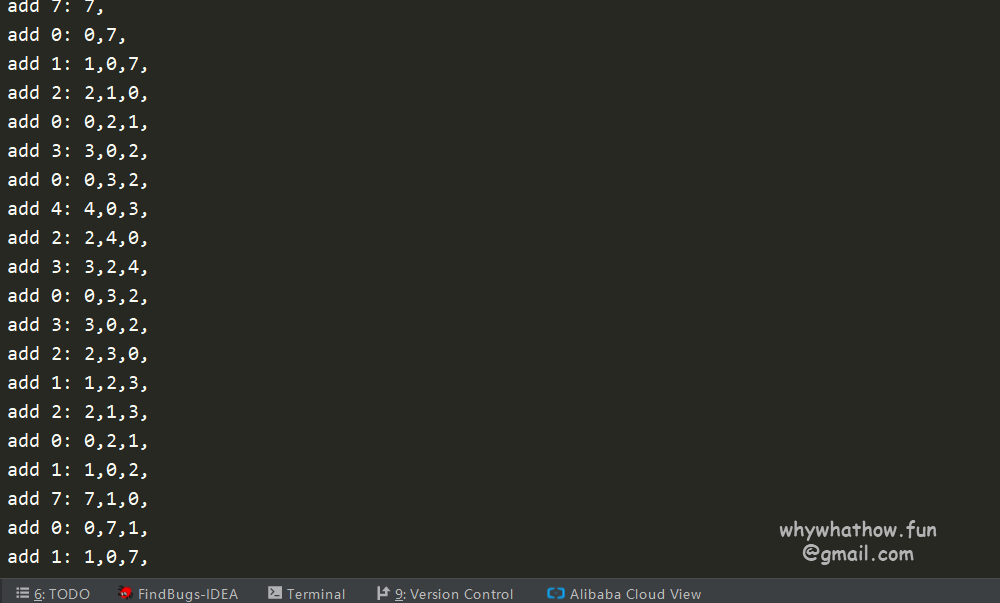
执行结果:

链表实现
思路: 头部插入, 尾部删除
头部元素: 最近访问的元素
尾部元素: 最近未被访问的元素.
时间复杂度分析:
- set() -> o(n) , //添加元素
- remove(index)->o(n),// 删除指定下标元素,
- remove()->0(1)// 删除尾部元素
- travel() -> o(n)// 遍历链表
性能分析:
由于链表顺序读的影响,导致查询节点的时间复杂度为o(n), 进而导致set() 的时间复杂度为o(n) 下一步的思想就是如何降低查找的时间复杂度.
代码实现:
代码地址: Here
package LRU;
import java.util.LinkedList;
/**
* @description: lru算法: 链表实现,set复杂度 o(n)
* @author: WhyWhatHow
* @create: 2020-05-03 07:09
**/
public class DemoLRULinkedList<T> {
/**
* lru算法实现: 最近最短时间内未被访问的数据被淘汰
*/
private LinkedList<T> list = new LinkedList();
// private T first, last;
private final static Integer MAX = 3;
private T get() {
return list.getFirst();
}
private T remove() {
return list.removeLast();
}
private void set(T t) {
int size = list.size();
// 判断插入元素是否在链表中, 是则移动元素,
int index = list.indexOf(t);
if (index != -1) {
// 移动元素
list.remove(index);
list.addFirst(t);
return;
}
// 判断链表是否已满,满,删除末尾元素
if (list.size() == MAX) {
list.removeLast();
}
// 不满,则末尾淘汰
list.addFirst(t);
}
private void travel() {
for (T t : list) {
System.out.print(t + ",");
}
System.out.println();
}
public static void main(String[] args) {
Integer[] a = new Integer[]{7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2, 1, 2, 0, 1, 7, 0, 1};
DemoLRULinkedList<Integer> lru = new DemoLRULinkedList<>();
for (int i = 0; i < a.length; i++) {
lru.set(a[i]);
System.out.print("add "+ a[i]+": ");
lru.travel();
}
}
}
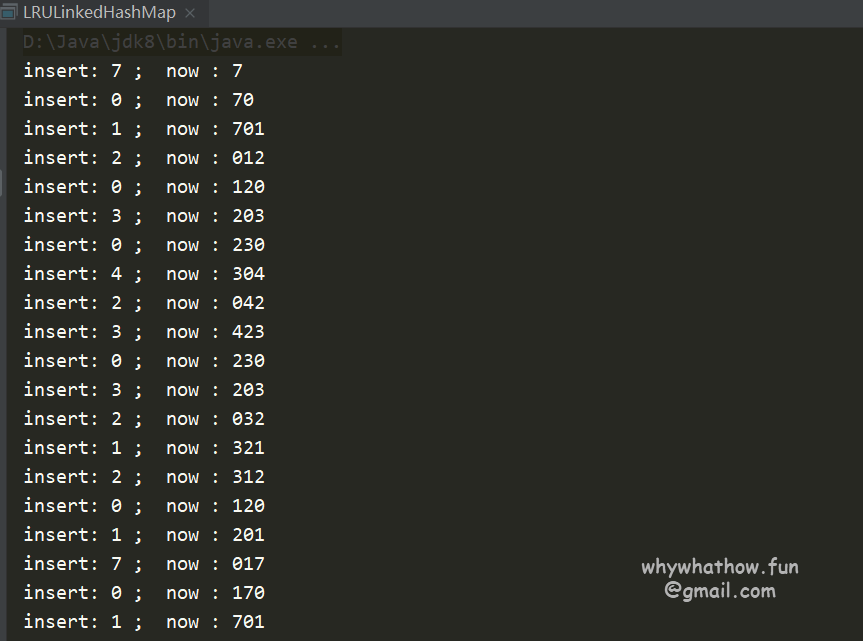
执行结果:
LinkedHashMap实现 LRU算法
思路: 通过hashmap 实现时已说明
时间复杂度分析:
put():
hashMap 的 put流程 时间复杂度为 o( ̄︶ ̄)o[看你怎么考虑,第一次插入,第一需要扩容,第一次需要链表转树(必要条件链表长度大于8并且table长度大于64)… ]
get(Object key):
super.get(key) 方法执行两步:
1. 第一步是查找getNode(int hash, Object key); 时间复杂度为o(n) ==ListNode|| o(nlogn) ==TreeNode
2. 第二步是移动节点到末尾afterNodeAccess(e); 时间复杂度 为 o(1) ; (因为hashmap有很多辅助节点)
代码实现:
代码地址: LRULinkedHashMap.class
package LRU;
import java.util.LinkedHashMap;
import java.util.Map;
/**
* @program: LeetCodeSolution
* @description: lru算法 通过linkedhashmap 实现查找o(1),增删o(1)的复杂度
* @author: WhyWhatHow
* @create: 2021-01-08 13:37
**/
public class LRULinkedHashMap<T> extends LinkedHashMap<T, T> {
private Integer len;
public LRULinkedHashMap(int initialCapacity,
float loadFactor,
boolean accessOrder) {
super(initialCapacity, loadFactor, accessOrder);
}
public Integer getLen() {
return len;
}
public void setLen(Integer len) {
this.len = len;
}
@Override
protected boolean removeEldestEntry(Map.Entry<T, T> eldest) {
return this.len < this.size();
}
void travel() {
this.keySet().forEach(System.out::print);
}
/**
* lru 算法描述:
* 1.在固定的容量下 即链表长度 假设
*/
public static void main(String[] args) {
Integer[] a = new Integer[]{7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2, 1, 2, 0, 1, 7, 0, 1};
LRULinkedHashMap<Integer> lruDemo = new LRULinkedHashMap<Integer>(16, 0.75f, true);
lruDemo.setLen(3);
for (Integer integer : a) {
lruDemo.put(integer, 1);
System.out.print("insert: " + integer + " ; now : ");
lruDemo.travel();
System.out.println();
}
}
}
执行结果:
HashMap+链表实现
利用数组实现, 插入时间复杂度为O(n)
有时间自己再来考虑实现.
思路:
hashMap: 存数据 保证查询速度o(1), 同步执行插入与删除.
链表: 也同样存数据,保证未节点为最近 访问的节点,头结点为待删除的节点.
参考:
https://leetcode-cn.com/problems/lru-cache/